بحث عن ط§ظ„ط§ط±طھط¨ط§ط· في ط§ظ„ط§ططµط§ط، ، ظ…ظˆط¶ظˆط¹ طھظ‚ط±ظٹط± عن الارتباط في الاحصاء ، بحث عن الارتباط في الاحصاء ، موضوع تقرير عن الارتباط في الاحصاء
الارتباط في الاحصاء
في نظرية الاحتمالات والإحصاء يبين الارتباط أو معامل الارتباط قوة العلاقة واتجاه العلاقة الخطية بين متغيرات عشوائية. أما استخدام المصطلح في المفهوم العام فيعبر عن أي علاقة وليس بالضرورة أن تكون خطية.
هناك عدة عوامل تستخدم في عدة حالات. أفضلها ما يعرف باسم معامل ارتباط جداء-عزم بيرسون (Pearson product-moment correlation coefficient) والذي يحصل عليه بقسمة التغاير لمتحولين على جداء انحرافهما المعياري، وعلى الرغم من اسم هذه الطريقة إلا أنه تم وضعها للمرة الأولى من قبل فرانسيس جالتون.[1]
هناك عدة عوامل تستخدم في عدة حالات. أفضلها ما يعرف باسم معامل ارتباط جداء-عزم بيرسون (Pearson product-moment correlation coefficient) والذي يحصل عليه بقسمة التغاير لمتحولين على جداء انحرافهما المعياري، وعلى الرغم من اسم هذه الطريقة إلا أنه تم وضعها للمرة الأولى من قبل فرانسيس جالتون.[1]
معامل ارتباط جداء-عزم بيرسون.
الخصائص الرياضية
يعرف معامل الارتباط ρX, Y بين متغيرن عشوائيين X و Y بقيم متوقعة μX و μY a و انحراف معياري σX و σY على الشكل:
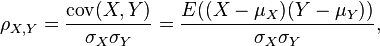 حيث E هي القيمة المتوقعة و cov تعني تغاير. هناك ترميز شائع مستخدم هو
حيث E هي القيمة المتوقعة و cov تعني تغاير. هناك ترميز شائع مستخدم هو
 وبما أنμX = E(X), σX2 = E[(X – E(X))2] = E(X2) − E2(X) and وبشكل مماثل لـ Y, فإننا نستطيع أن نكتب أيضاً
وبما أنμX = E(X), σX2 = E[(X – E(X))2] = E(X2) − E2(X) and وبشكل مماثل لـ Y, فإننا نستطيع أن نكتب أيضاً
 من الممكن تعريف الارتباط فقط إذا كان كلا الانحرافان المعياريان منتهيان وكلاهما لا يساوي الصفر.
من الممكن تعريف الارتباط فقط إذا كان كلا الانحرافان المعياريان منتهيان وكلاهما لا يساوي الصفر.